Linear Equations

A linear equation is an equation for a straight line

These are all linear equations:

		y = 2x + 1
		5x = 6 + 3y
		y/2 = 3 − x

Let us look more closely at one example:

Example: y = 2x + 1 is a linear equation:

line on a graph

The graph of y = 2x+1 is a straight line

When x increases, y increases twice as fast, so we need 2x
When x is 0, y is already 1. So +1 is also needed
And so: y = 2x + 1

Here are some example values:

x	y = 2x + 1
-1	y = 2 × (-1) + 1 = -1
0	y = 2 × 0 + 1 = 1
1	y = 2 × 1 + 1 = 3
2	y = 2 × 2 + 1 = 5

Check for yourself that those points are part of the line above!

Different Forms

There are many ways of writing linear equations, but the key idea is:

Variables are only to the first power (x, y, and so on),
Variables are not multiplied together (no xy),
No variables in denominators (no 1x and so on)

Examples: These are linear equations:

		y = 3x − 6
		y − 2 = 3(x + 1)
		y + 2x − 2 = 0
		5x = 6
		y/2 = 3

But the variables (like "x" or "y") in Linear Equations do NOT have:

Exponents (like the 2 in x²)
Square roots, cube roots, and so on

Examples: These are NOT linear equations:

		y² − 2 = 0
		3√x − y = 6
		x³/2 = 16
		xy = 1

Slope-Intercept Form

The most common form is the slope-intercept equation of a straight line:

y=mx+b graph


Slope (or Gradient)	Y Intercept

Example: y = 2x + 1

Slope: m = 2
Intercept: b = 1

Play With It !

You can see the effect of different values of m and b at Explore the Straight Line Graph

Point-Slope Form

Another common one is the Point-Slope Form of the equation of a straight line:

y − y₁ = m(x − x₁)

Point-Slope Form

Example: y − 3 = (¼)(x − 2)

It is in the form y − y₁ = m(x − x₁) where:

y₁ = 3
m = ¼
x₁ = 2

General Form

And there is also the General Form of the equation of a straight line:

Ax + By + C = 0

(A and B cannot both be 0)

Example: 3x + 2y − 4 = 0

It is in the form Ax + By + C = 0 where:

A = 3
B = 2
C = −4

There are other, less common forms as well.

As a Function

Sometimes a linear equation is written as a function, with f(x) instead of y:

y = 2x − 3

f(x) = 2x − 3

These are the same!

And functions are not always written using f(x):

y = 2x − 3

w(u) = 2u − 3

h(z) = 2z − 3

These are also the same!

The Identity Function

There is a special linear function called the "Identity Function":

f(x) = x

And here is its graph:

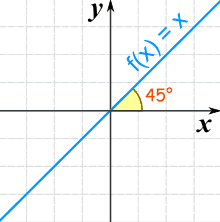
Identity Function
It makes a 45° (its slope is 1)

It is called "Identity" because what comes out is identical to what goes in:

In	Out
0	0
5	5
−2	−2
...and so on	...and so on

Constant Functions

Another special type of linear function is the Constant Function ... it is a horizontal line:

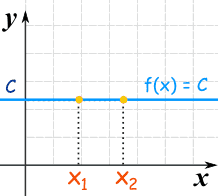
Constant Function

f(x) = C

No matter what value of "x", f(x) is always equal to some constant value.

Using Linear Equations

You may like to read some of the things you can do with lines:

519, 2074, 1158, 2075, 520, 1159, 2455, 2456, 2457, 2458