Equation of a Line from 2 Points

First, let's see it in action. Here are two points (you can drag them) and the equation of the line through them. Explanations follow.

../geometry/images/geom-line-equn.js

The Points

We use Cartesian Coordinates to mark a point on a graph by how far along and how far up it is:

graph with point (12,5)
Example: The point (12,5) is 12 units along, and 5 units up

Steps

There are 3 steps to find the Equation of the Straight Line :

1. Find the slope of the line
2. Put the slope and one point into the "Point-Slope Formula"
3. Simplify

Step 1: Find the Slope (or Gradient) from 2 Points

What is the slope (or gradient) of this line?

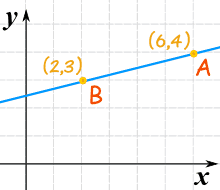
graph 2 points

We know two points:

point "A" is (6,4) (at x is 6, y is 4)
point "B" is (2,3) (at x is 2, y is 3)

The slope is the change in height divided by the change in horizontal distance.

Looking at this diagram ...

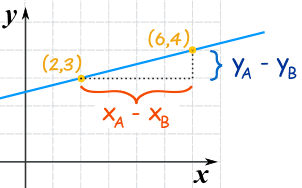
graph 2 points

Slope m = change in ychange in x = y_A − y_Bx_A − x_B

In other words, we:

subtract the Y values,
subtract the X values
then divide

Like this:

m = change in y change in x = 4−3 6−2 = 1 4 = 0.25

It doesn't matter which point comes first, it still works out the same. Try swapping the points:

m = change in y change in x = 3−4 2−6 = −1 −4 = 0.25

Same answer.

Step 2: The "Point-Slope Formula"

Now put that slope and one point into the "Point-Slope Formula"

graph 2 points

Start with the "point-slope" formula (x₁ and y₁ are the coordinates of a point on the line):

y − y₁ = m(x − x₁)

We can choose any point on the line for x₁ and y₁, so let's just use point (2,3):

y − 3 = m(x − 2)

We already calculated the slope "m":

m = change in ychange in x = 4−36−2 = 14

And we have:

y − 3 = 14(x − 2)

That is an answer, but we can simplify it further.

Step 3: Simplify

Start with:y − 3 = 14(x − 2)

Multiply 14 by (x−2):y − 3 = x4 − 24

Add 3 to both sides:y = x4 − 24 + 3

Simplify:y = x4 + 52

And we get:

y = x4 + 52

Which is now in the Slope-Intercept (y = mx + b) form.

Check It!

Let us confirm by testing with the second point (6,4):

y = x/4 + 5/2 = 6/4 + 2.5 = 1.5 + 2.5 = 4

Yes, when x=6 then y=4, so it works!

Another Example

Example: What is the equation of this line?

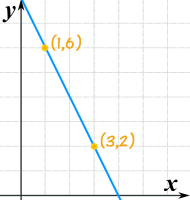
graph 2 points

Start with the "point-slope" formula:

y − y₁ = m(x − x₁)

Put in these values:

x₁ = 1
y₁ = 6
m = (2−6)/(3−1) = −4/2 = −2

And we get:

y − 6 = −2(x − 1)

Simplify to Slope-Intercept (y = mx + b) form:

y − 6 = −2x + 2

y = −2x + 8

DONE!

The Big Exception

The previous method works nicely except for one particular case: a vertical line:

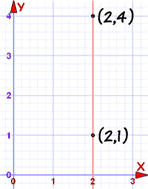
graph vertical line

A vertical line's gradient is undefined (because we cannot divide by 0):

m = y_A − y_Bx_A − x_B = 4 − 12 − 2 = 30 = undefined

But there is still a way of writing the equation: use x= instead of y=, like this:

x = 2

7270, 525, 526, 1165, 1166, 7291, 7292, 7300, 7301, 7302