Exponential Function Reference
This is the general Exponential Function (see below for ex):
f(x) = ax
a is any value greater than 0
Properties depend on value of "a"
- When a=1, the graph is a horizontal line at y=1
- Apart from that there are two cases to look at:
a between 0 and 1
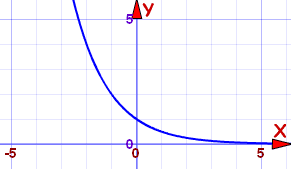
Example: f(x) = (0.5)x
For a between 0 and 1
- As x increases, f(x) heads to 0
- As x decreases, f(x) heads to infinity
- It is a Strictly Decreasing function (and so is "Injective")
- It has a Horizontal Asymptote along the x-axis (y=0)
a above 1
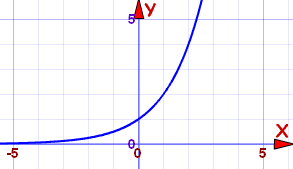
Example: f(x) = (2)x
For a above 1:
- As x increases, f(x) heads to infinity
- As x decreases, f(x) heads to 0
- it is a Strictly Increasing function (and so is "Injective")
- It has a Horizontal Asymptote along the x-axis (y=0)
Plot the graph here (use the "a" slider)
In General:
- It is always greater than 0, and never crosses the x-axis
- It always intersects the y-axis at y=1 ... in other words it passes through (0,1)
- At x=1, f(x)=a ... in other words it passes through (1,a)
- It is an Injective (one-to-one) function
Its Domain is the Real Numbers:
Its Range is the Positive Real Numbers: (0, +∞)
Inverse
ax is the inverse function of loga(x) (the Logarithmic Function)
So the Exponential Function can be "reversed" by the Logarithmic Function.
The Natural Exponential Function
This is the "Natural" Exponential Function:
f(x) = ex
Where e is "Eulers Number" = 2.718281828459... and so on
Graph of f(x) = ex
The value e is important because it creates these useful properties:
At any point the slope of ex equals the value of ex :
when x=0, the value of ex = 1, and slope = 1
when x=1, the value of ex = e, and slope = e
and so on...
The area up to any x-value is also equal to ex :