Marther's Vineyard - Solution

Puzzles -> Sam Loyd Puzzles

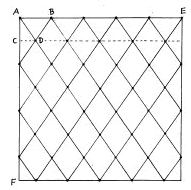
The Puzzle: What are the maximum number of grape vines that can be planted, not closer than nine feet apart, in a square plot containing one-sixteenth of an acre?

(Note: each side of this square plot would be 52 feet 2 inches)

.
.
.
.
(Scroll down if you really want
to see the Solution ...)
.
.
.
.
.
.

The Solution . . .

By drawing a line on the bias as shown in the adjoining diagram, from one corner to another, and crossing and paralleling the same, it will be found that 41 vines can be planted, a little over nine feet apart, and well within the fence line.

Discuss this puzzle at our Forum