Equivalent Fractions

Equivalent Fractions have the same value, even though they may look different.

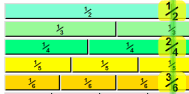
These fractions are really the same:

1 2   =   2 4   =   4 8

Why are they the same? Because when you multiply or divide both the top and bottom by the same number, the fraction keeps it's value.

The rule to remember is:

"Change the bottom using multiply or divide,
And the same to the top must be applied"

Here is why those fractions are really the same:

	× 2		× 2
12   =   24   =   48
	× 2		× 2

1/2		2/4		4/8
	=		=

See Fractions on the Number Line ...

... it shows many equivalent fractions.

Also see the Chart of Fractions with many examples of equivalent fractions.

Dividing

Here are some more equivalent fractions, this time by dividing:

	÷ 3		÷ 6
1836   =   612   =   12
	÷ 3		÷ 6

Choose the number you divide by carefully, so that the results (both top and bottom) stay whole numbers.

If we keep dividing until we can't go any further, then we have simplified the fraction (made it as simple as possible).

Summary:

• You can make equivalent fractions by multiplying or dividing both top and bottom by the same amount.
• You only multiply or divide, never add or subtract, to get an equivalent fraction.
• Only divide when the top and bottom stay as whole numbers.