Stationary Points

Also called "Critical Points"

In a smoothly changing function a Stationary Point is a point where the function stops increasing or decreasing:

function local minimum and maximum

It can be a:

Bike on Trail

Where is it flat?  Where the slope is zero.

Where is the slope zero?  Where the derivative is zero

Let's dive right in with an example:

quadratic graph

Example: A ball is thrown in the air. Its height at any time t is given by:

h = 3 + 14t − 5t2

What is its maximum height?

 

Using derivatives we can find the slope of that function:

h' = 0 + 14 − 5(2t)
= 14 − 10t

(See below this example for how we found that derivative.)

 

quadratic graph

Now find when the slope is zero:

14 − 10t = 0
10t = 14
t = 14 / 10 = 1.4

The slope is zero at t = 1.4 seconds

And the height at that time is:

h = 3 + 14×1.4 − 5×1.42
h = 3 + 19.6 − 9.8 = 12.8

And so:

The maximum height is 12.8 m (at t = 1.4 s)

A Quick Refresher on Derivatives

A derivative basically finds the slope of a function.

In the previous example we took this:

h = 3 + 14t − 5t2

and came up with this derivative:

h' = 0 + 14 − 5(2t)
= 14 − 10t

this is the slope of the function at any time t

slope examples: y=3, slope=0; y=2x, slope=2

Using these Derivative Rules:

  • The slope of a constant value (like 3) is 0
  • The slope of a line like 2x is 2, so 14t has a slope of 14
  • A square function like t2 has a slope of 2t, so 5t2 has a slope of 5(2t)
  • And then we added them up: 0 + 14 − 5(2t)

What Type of Stationary Point?

We saw it on the graph, it was a Maximum!

But otherwise: derivatives come to the rescue again.

Take the derivative of the slope (the second derivative of the original function):

The Derivative of 14 − 10t is −10

This means the slope is continually getting smaller (−10): traveling from left to right the slope starts out positive (the function rises), goes through zero (the flat point), and then becomes negative (the function falls):

slope positive then zero then negative
A slope that gets smaller (and goes through 0) means a maximum.

This is called the Second Derivative Test

On the graph above I showed the slope before and after, but in practice we do the test at the point where the slope is zero:

Second Derivative Test

When a function's slope is zero at x, and the second derivative at x is:

  • less than 0, it is a local maximum
  • greater than 0, it is a local minimum
  • equal to 0, then the test fails (there may be other ways of finding out though)

 

Second Derivative:
less than 0 is a maximum
greater than 0 is a minimum

 

Example: Find the maxima and minima for:

y = 5x3 + 2x2 − 3x

The derivative (slope) is:

y' = 15x2 + 4x − 3

It is Quadratic.

We can use the Quadratic Equation Solver to find it is zero at:

  • x = −3/5
  • x = +1/3

Could they be maxima or minima? (Don't look at the graph yet!)

 

The second derivative is y'' = 30x + 4

At x = −3/5:

y'' = 30(−3/5) + 4 = −14
it is less than 0, so −3/5 is a local maximum

At x = +1/3:

y'' = 30(+1/3) + 4 = +14
it is greater than 0, so +1/3 is a local minimum

(Now you can look at the graph.)

5x^3 2x^2 3x

Steps

Example: The parabola f(x) = −x2 + 4x

  • The derivative of this function is f'(x) = −2x + 4
  • Solve the derivative equation f'(x) = −2x + 4 = 0, and we get x = 2
  • Take the second derivative f''(x) = −2, which is always negative, so it is a local maximum

There is a local maximum at x = 2

One More Example

Example: Find the maxima and minima for:

y = x3 − 6x2 + 12x − 5

The derivative is:

y' = 3x2 − 12x + 12

So we want to solve:

3x2 − 12x + 12 = 0

It is a Quadratic Equation. We can solve it using the Quadratic Equation Solver to get only one zero at x = 2

Is it a maximum or minimum?

The second derivative is y'' = 6x − 12

At x = 2:

y'' = 6(2) − 12 = 0
it is 0, so the test fails

And here is why:

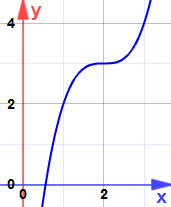
x^3 6x^2 12x 5

It is an Inflection Point ("saddle point") ... the slope does become zero, but it is neither a maximum nor minimum.

 

Must Be Differentiable

And there is an important technical point:

The function must be differentiable (the derivative must exist at each point in its domain).

Example: How about the function f(x) = |x| (absolute value) ?

  |x| looks like this:   Absolute Value function

At x=0 it has a sharp point!

In fact it is not differentiable there (as shown on the differentiable page).

So we can't use the derivative method for the absolute value function.

The function must also be continuous, but any function that is differentiable is also continuous, so we are covered.

 

8915, 8916, 8917, 8921, 8922, 8924, 8918, 8919, 8920, 8923
Finding Maxima and Minima using Derivatives Calculus Index