Continuous Functions

A function is continuous when its graph is a single unbroken curve ...

... that you could draw without lifting your pen from the paper.

That is not a formal definition, but it helps you understand the idea.

Here is a continuous function:

continuous polynomial

Examples

So what is not continuous (also called discontinuous) ?

Look out for holes, jumps or vertical asymptotes (where the function heads up/down towards infinity).

Not Continuous
(hole)

Not Continuous
(jump)

Not Continuous
(vertical asymptote)

Try these different functions so you get the idea:

(Use slider to zoom, drag graph to reposition, click graph to re-center.)

Domain

doman and range

A function has a Domain.

In its simplest form the domain is all the values that go into a function.

We may be able to choose a domain that makes the function continuous

Example: 1/(x−1)

At x=1 we have:

1/(1−1) = 1/0 = undefined

So there is a "discontinuity" at x=1

continuous asymptote
f(x) = 1/(x−1)

So f(x) = 1/(x−1) over all Real Numbers is NOT continuous

Let's change the domain to x>1

continuous asymptote exclude
g(x) = 1/(x−1) for x>1

So g(x) IS continuous

In other words g(x) does not include the value x=1, so it is continuous.

When a function is continuous within its Domain, it is a continuous function.

More Formally !

We can define continuous using Limits (it helps to read that page first):

A function f is continuous when, for every value c in its Domain:

f(c) is defined,

and

limx→cf(x) = f(c)

"the limit of f(x) as x approaches c equals f(c)"

The limit says:

"as x gets closer and closer to c
then f(x) gets closer and closer to f(c)"

And we have to check from both directions:

as x approaches c (from left) then f(x) approaches f(c)

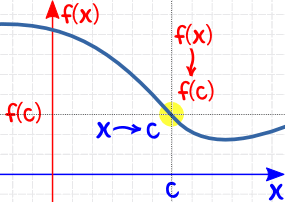AND as x approaches c (from right) then f(x) approaches f(c)

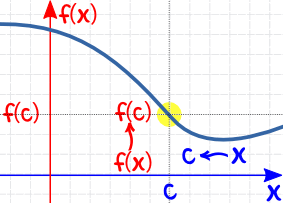If we get different values from left and right (a "jump"), then the limit does not exist!

And remember this has to be true for every value c in the domain.

How to Use:

Make sure that, for all x values:

f(x) is defined
and the limit at x equals f(x)

Here are some examples:

Example: f(x) = (x²−1)/(x−1) for all Real Numbers

graph (x^2-1)/(x-1) hole

The function is undefined when x=1:

(x²−1)/(x−1) = (1²−1)/(1−1) = 0/0

So it is not a continuous function

Let us change the domain:

Example: g(x) = (x²−1)/(x−1) over the interval x<1

Almost the same function, but now it is over an interval that does not include x=1.

So now it is a continuous function (does not include the "hole")

Example: How about this piecewise function:

h(x) = { 2 if x<=1, x if x>1 }

It looks like this:

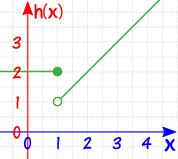
continuous jump graph

It is defined at x=1, because h(1)=2 (no "hole")

But at x=1 you can't say what the limit is, because there are two competing answers:

"2" from the left, and
"1" from the right

so in fact the limit does not exist at x=1 (there is a "jump")

And so the function is not continuous.

But:

Example: How about the absolute value piecewise function:

Absolute Value function

At x=0 it has a very pointy change!

But it is still defined at x=0, because f(0)=0 (so no "hole"),

And the limit as you approach x=0 (from either side) is also 0 (so no "jump"),

So it is in fact continuous.

(But it is not differentiable at x=0)