Piecewise Functions
A Function Can be in Pieces
We can create functions that behave differently based on the input (x) value.
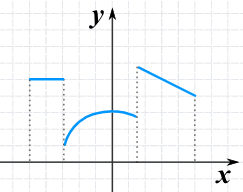
A function made up of 3 pieces
Example: Imagine a function
- when x is less than 2, it gives x2,
- when x is exactly 2 it gives 6
- when x is more than 2 and less than or equal to 6 it gives the line 10−x
It looks like this:
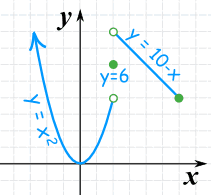
(a solid dot means "including",
an open dot means "not including")
And we write it like this:
The Domain (all the values that can go into the function) is all Real Numbers up to and including 6, which we can write like this:
- using Interval Notation: Dom(f) = (-∞, 6]
- using Set Builder Notation: Dom(f) = {x ∈ | x ≤ 6}
And here are some example values:
| X | Y |
|---|---|
| −4 | 16 |
| −2 | 4 |
| 0 | 0 |
| 1 | 1 |
| 2 | 6 |
| 3 | 7 |
Example: Here is another piecewise function:
| which looks like: | 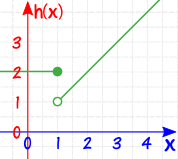 |
What is h(−1)?
x is ≤ 1, so we use h(x) = 2, so h(−1) = 2
What is h(1)?
x is ≤ 1, so we use h(x) = 2, so h(1) = 2
What is h(4)?
x is > 1, so we use h(x) = x, so h(4) = 4
Piecewise functions let us make functions that do anything we want!
Example: A Doctor's fee is based on the length of time.
- Up to 6 minutes costs $50
- Over 6 and up to 15 minutes costs $80
- Over 15 minutes costs $80 plus $5 per minute above 15 minutes
Which we can write like this:
You visit for 12 minutes, what is the fee? $80
You visit for 20 minutes, what is the fee? $80+$5(20-15) = $105
The Absolute Value Function
The Absolute Value Function is a famous Piecewise Function.
It has two pieces:
- below zero: -x
- from 0 onwards: x
f(x) = |x|
The Floor Function
The Floor Function is a very special piecewise function. It has an infinite number of pieces:
The Floor Function
