Partial Sums
A Partial Sum is a Sum of Part of a Sequence.
Example:
This is the Sequence of even numbers: {2, 4, 6, 8, 10, 12, ...}
This is the Partial Sum of the first 4 terms of that sequence: 2+4+6+8 = 20
Let us define things a little better now:
A Sequence is a set of things (usually numbers) that are in order.
 |
A Partial Sum is the sum of part of the sequence
Language Note: A "Series" is the sum of all the terms in an infinite sequence.
So Partial Sums are sometimes called "Finite Series"
Sigma
Partial Sums are often written down using Σ to mean "add them all up":
 |
This symbol (called Sigma) means "sum up" |
| So | |
means to sum things up ... |
Sum What?Sum whatever appears after the Sigma: |
 |
so we sum n | ||
But What is the Value of n ?The values are shown below |
 |
it says n goes from 1 to 4, so that is 1, 2, 3 and 4 |
||
OK, Let's Go ...So now we add up 1,2,3 and 4: |
 |
|||
Here it is in one diagram:
More Powerful
But Σ can do more powerful things than that!
You could square n each time and sum the result:
You could "add up the first four terms in the sequence 2n+1":
And you don't have to use n. Here we use i and sum up i × (i+1), going from 1 to 3:
And you can start and end with any number. Here we go from 3 to 5:
Properties
Partial Sums have some useful properties that can help you.
Multiplying by a Constant Property
Say you have something you want to sum up, let's call it ak
ak could be k2, or k(k-7)+2, or ... anything really
And c is some constant value (like 2, or -9.1, etc), then:
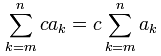
In other words: if every term you are summing is multiplied by a constant, you can "pull" the constant outside the sigma.
Example:
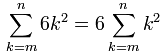
So instead of summing 6k2 you can sum k2 and then multiply the whole result by 6
Adding or Subtracting Property
Here is another useful fact:
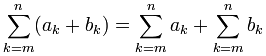
Which means that when two terms are added together, and you want to sum them up, you can actually sum them separately and then add the results.
Example:
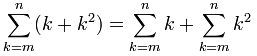
It is going to be easier to do the two sums and then add them at the end.
Note this also works for subtraction:
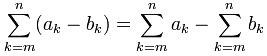
Useful Shortcuts
And here are some useful shortcuts that make the sums a lot easier.
In each case you are trying to sum from 1 to some value n.
 |
Summing 1 equals n | |
 |
Summing the constant c equals c times n | |
 |
A shortcut when summing k | |
 |
A shortcut when summing k2 | |
 |
A shortcut when summing k3 |
Let us now use some of those:
Example 1: You sell concrete blocks for landscaping.
A customer says they will buy the entire "pyramid" of blocks you keep out front. The stack is 14 blocks high.
How many blocks are in there?
 |
Each layer is a square, so the calculation is: 12 + 22 + 32 + ... + 142 But this can be written much more easily as:
|
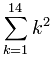
We can use the formula for k2 from above:
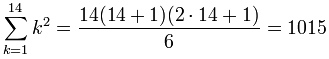
That was a lot easier than adding up 12 + 22 + 32 + ... + 142.
And here is a more complicated example:
Example 2: The customer wants a better price.
The customer says the blocks on the outside of the pyramid should be cheaper, as they need cleaning.
You agree to:
- $7 for outer blocks
- and $11 for inner blocks.
What is the total cost?
 |
You can calculate how many "inner" and "outer" blocks in any layer (except the first) using
|
And so the cost per layer is:
- cost (outer blocks) = $7 × 4(size-1)
- cost (inner blocks) = $11 × (size-2)2
So all layers together (except first) will cost:
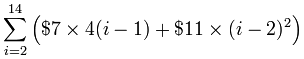
Now we have the sum, let us try to make the calculations easier!
Using the "Addition Property" from above:
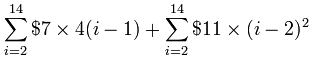
Using the "Multiply by Constant Property" from above:
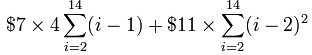
That is good ... but we can't use any shortcuts as it is, as we are going from i=2 instead of i=1
HOWEVER, if we invent two new variables:
- j = i-1
- k = i-2
We have:
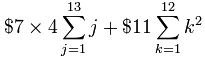
(I dropped the k=0 case, because I know that 02=0)
And now we can use the shortcuts:
After a little calculation:
$7 × 364 + $11 × 650 = $9,698.00
Oh! And don't forget the top layer (size=1) which is just one block. Maybe you can give them that one for free, you are so generous!
Note: as a check, when we add the "outer" and "inner" blocks, plus the one on top, we get
364 + 650 + 1 = 1015
Which is the same number we got for the "total blocks" before ... yay!