Infinite Series

The sum of infinite terms that follow a rule.

When we have an infinite sequence of values:

12 , 14 , 18 , 116 , ...

which follow a rule (in this case each term is half the previous one),

and we add them all up:

12 + 14 + 18 + 116 + ... = S

we get an infinite series.

(Note: The dots "..." mean "continuing on indefinitely")

A Sequence is a list of numbers. A Series is what we get when we add them up.

First Example

Adding up an infinite number of things sounds like it would take forever (literally!) but math gives us shortcuts.

Let's use our example from above:

12 + 14 + 18 + 116 + ... = 1

And here's why:

Large square divided into rectangles of area 1/2, 1/4, 1/8, and so on, filling the whole square.
(We also show a proof using Algebra below)

Notation

We often use Sigma Notation for infinite series. Our example from above looks like:

∞

n=1

12ⁿ = 12 + 14 + 18 + 116 + ... = 1

The symbol Σ means "sum up"

Try putting 1/2^n into the Sigma Calculator.

Another Example

14 + 116 + 164 + 1256 + ... = 13

Each term is a quarter of the previous one, and the sum equals 1/3:

Square divided into L-shaped regions of 3 squares each, with 1 square colored in each region.

Looking at the image: at every step, we color 1 square and leave 2 squares of the same size empty. Since the colored part is always 1 out of 3 equal parts, the total colored area ends up being 13.

(By the way, this one was worked out by Archimedes over 2200 years ago.)

Converge

Let's add the terms one at a time, in order. When the "sum so far" approaches a finite value, the series is said to be "convergent":

Our first example:

12 + 14 + 18 + 116 + ...

Adds up like this:

Term		Sum so far
1/2		0.5
1/4		0.75
1/8		0.875
1/16		0.9375
1/32		0.96875
...		...

The sums are heading toward a value (1 in this case), so this series is convergent.

The "sum so far" is called a partial sum .

So, more formally, we say it is a convergent series when:

"the sequence of partial sums has a finite limit (the value it gets closer and closer to)."

For a series to converge, the terms in the sequence must get smaller and smaller, but that doesn't always guarantee the series will converge! (Wait until you see the Harmonic Series below).

Diverge

If the sums don't converge, the series is said to diverge.

It can go to +infinity, −infinity or just go up and down without settling on any value.

Example:

1 + 2 + 3 + 4 + ...

Adds up like this:

Term		Sum so far
1		1
2		3
3		6
4		10
5		15
...		...

The sums are just getting larger and larger, not heading to any finite value.

It doesn't converge, so it is divergent, and heads to infinity.

Example: 1 − 1 + 1 − 1 + 1 ...

It goes up and down without settling toward some value, so it is divergent.

More Examples

Arithmetic Series

When the difference between each term and the next is a constant, it is called an arithmetic series.

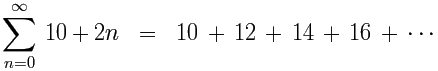
Sigma n=0 to infinity of (10+2n) = 10+12+14+...

(The difference between each term is 2.)

Geometric Series

When the ratio between each term and the next is a constant, it is called a geometric series.

Our first example from above is a geometric series:

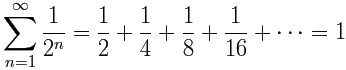
Sigma notation for the sum from n=1 to infinity of (1/2)^n.

(The ratio between each term is ½)

And, as promised, we can show you why that series equals 1 using Algebra:

First, we'll call the whole sum "S": S = 1/2 + 1/4 + 1/8 + 1/16 + ... Next, divide S by 2:S/2 = 1/4 + 1/8 + 1/16 + 1/32 + ...

Now subtract S/2 from S

All the terms from 1/4 onwards cancel out.

And we get:S − S/2 = 1/2 Simplify: S/2 = 1/2 And so:S = 1

Harmonic Series

This is the Harmonic Series:

∞

n=1

1n = 1 + 12 + 13 + 14 + 15 + ...

It is divergent.

How do we know? Let's compare it to another series.

We group the terms so each group adds up to at least 12:

1	+	12	+	13+14	+	15+16+17+18	+	19+...

1	+	12	+	14+14	+	18+18+18+18	+	116+...

In each case, the top values are equal or greater than the bottom ones.

Now, let's add up the bottom groups:

1	+	12	+	14+14	+	18+18+18+18	+	116+...

1	+	12	+	12	+	12	+	12	+	... = ∞

That series is divergent.

So the harmonic series must also be divergent.

Here's another way:

We can sketch the area of each term and compare it to the area under the 1/x curve:

Bar graph of 1 + 1/2 + 1/3 + 1/4 showing bars are always taller than the curve y=1/x.
1/x vs harmonic series area

Calculus tells us the area under 1/x (from 1 onwards) approaches infinity, and the harmonic series is greater than that, so it must be divergent.

Alternating Series

An Alternating Series has terms that alternate between positive and negative.

It may or may not converge.

Example: 12 − 14 + 18 − 116 + ... = 13

This illustration may convince you that the terms converge on 13:

Number line showing arrows jumping back and forth, narrowing down to the value 1/3.

Maybe you can try to prove it yourself? Try pairing up each plus and minus pair, then look up above for a series that matches.

Another example of an Alternating Series (based on the Harmonic Series above):

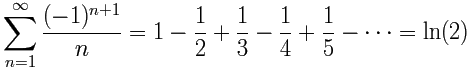
Sigma n=1 to infinity of (-1)^(n+1) /n = 1 - 1/2 + 1/3 - 1/4 + ... = ln(2)

This one converges on the natural logarithm of 2

Advanced Explanation:

To show WHY, first we start with a square of area 1, and then pair up the minus and plus fractions to show how they cut the area down to the area under the curve y=1/x between 1 and 2:

Diagram pairing positive and negative blocks to fit under the curve of 1/x from x=1 to 2.

Can you see what remains is the area of 1/x from 1 to 2?

Using integral calculus (trust me) that area is ln(2):

1/x dx = ln(2) − ln(1) = ln(2)

You can investigate this further!

do those rectangles really make the area above the curve as shown?
is the area below the curve really ln(2) = 0.693... ? Try the Integral Approximation Calculator to see (y=1/x between 1 and 2)

Order!

The order of the terms can be very important! We can sometimes get weird results when we change their order.

For example in an alternating series, what if we made all positive terms come first? So be careful!

There are other types of Infinite Series, and it is interesting (and often challenging!) to work out if they are convergent or not, and what they may converge to.