Inverse of a Matrix
using Minors, Cofactors and Adjugate

Note: also check out Matrix Inverse by Row Operations and the Matrix Calculator

We can calculate the Inverse of a Matrix by:

• Step 1: calculating the Matrix of Minors,
• Step 2: then turn that into the Matrix of Cofactors,
• Step 3: then the Adjugate, and
• Step 4: multiply that by 1/Determinant.

But it is best explained by working through an example!

Example: find the Inverse of A:

It needs 4 steps. It is all simple arithmetic but there is a lot of it, so try not to make a mistake!

Step 1: Matrix of Minors

The first step is to create a "Matrix of Minors". This step has the most calculations.

For each element of the matrix:

• ignore the values on the current row and column
• calculate the determinant of the remaining values

Put those determinants into a matrix (the "Matrix of Minors")

Determinant

For a 2×2 matrix (2 rows and 2 columns) the determinant is easy: ad-bc

Think of a cross: Blue means positive (+ad), Red means negative (-bc)

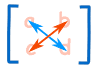(It gets harder for a 3×3 matrix, etc)

The Calculations

Here are the first two, and last two, calculations of the "Matrix of Minors" (notice how I ignore the values in the current row and columns, and calculate the determinant using the remaining values):

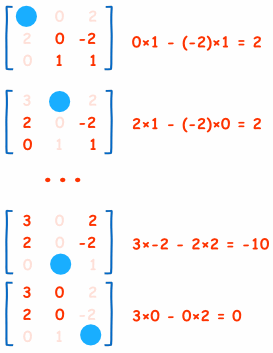
And here is the calculation for the whole matrix:

Step 2: Matrix of Cofactors

This is easy! Just apply a "checkerboard" of minuses to the "Matrix of Minors". In other words, we need to change the sign of alternate cells, like this:

Step 3: Adjugate (also called Adjoint)

Now "Transpose" all elements of the previous matrix... in other words swap their positions over the diagonal (the diagonal stays the same):

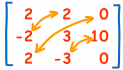
Step 4: Multiply by 1/Determinant

Now find the determinant of the original matrix. This isn't too hard, because we already calculated the determinants of the smaller parts when we did "Matrix of Minors".

Using:

Elements of top row: 3, 0, 2
Minors for top row: 2, 2, 2

We end up with this calculation:

Determinant = 3×2 − 0×2 + 2×2 = 10

Your Turn: try this for any other row or column, you should also get 10.

Now we multiply the Adjugate by 1/Determinant to get:

And we are done!

Compare this answer with the one we got on Inverse of a Matrix using Elementary Row Operations. Is it the same? Which method do you prefer?

Larger Matrices

It is exactly the same steps for larger matrices (such as a 4×4, 5×5, etc), but wow! there is a lot of calculation involved.

For a 4×4 Matrix we have to calculate 16 3×3 determinants. So it is often easier to use computers (such as the Matrix Calculator.)

Conclusion

• For each element, calculate the determinant of the values not on the row or column, to make the Matrix of Minors
• Apply a checkerboard of minuses to make the Matrix of Cofactors
• Transpose to make the Adjugate
• Multiply by 1/Determinant to make the Inverse