Prime Numbers and Composite Numbers

Prime Numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, more...

jpMYfW9XziU

A Prime Number is:

a whole number above 1 that can't be made by multiplying smaller whole numbers

Example: 5 is a prime number.

We can't multiply smaller whole numbers (like 2, 3 or 4) to make 5

Example: 6 is not a prime number.

We can multiply 2×3 to make 6, so 6 isn't a prime number, it is a composite number

Not 1

Years ago 1 was included as a Prime, but now it isn't:

1 is not Prime and also not Composite.

Dividing Into Equal Groups

It is all about trying to divide the number into equal groups

Some whole numbers can be divided up exactly, and some can't!

Example: 6

6 can be divided exactly by 2, or by 3:

6 = 2 × 3

Like this:

Six dots arranged in two equal rows of three

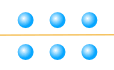
divided into 2 groups

Six dots arranged in three equal rows of two

divided into 3 groups

Example: 7

But 7 can't be divided up exactly:

Seven dots arranged in two rows of three with one leftover dot, showing it cannot be divided equally

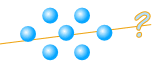
And we give them names:

When a number can be divided up exactly it is a Composite Number
When a number can't be divided up exactly it is a Prime Number

So 6 is Composite, but 7 is Prime

Like this:

Visual blocks for numbers 2 to 7, showing prime numbers as single blocks and composites as combined blocks

And that explains it ... but there are some more details ...

Not Into Fractions

We are only dealing with whole numbers here! We aren't going to cut things into halves or quarters.

Not Into Groups of 1

OK, we could have divided 7 into seven 1s (or one 7) like this:

7 = 1 x 7

But we could do that for any whole number!

So we are only interested in dividing by whole numbers other than the number itself.

Example: is 7 a Prime Number or Composite Number?

Seven dots arranged in two rows of three with one leftover dot, showing it cannot be divided equally

We can't divide 7 exactly by 2 (we get 2 lots of 3, with one left over)
We can't divide 7 exactly by 3 (we get 3 lots of 2, with one left over)
We can't divide 7 exactly by 4, or 5, or 6

We can only divide 7 into one group of 7 (or seven groups of 1):

7 = 1 x 7

So 7 is a Prime Number

And also:

It is a Composite Number when it can be divided exactly by a whole number other than itself.

Like this:

Example: is 6 a Prime Number or Composite Number?

6 can be divided exactly by 2, or by 3, as well as by 1 or 6:

6 = 1 × 6
6 = 2 × 3

So 6 is a Composite Number

Sometimes a number can be divided exactly in many ways:

Example: 12 can be divided exactly by 1, 2, 3, 4, 6 and 12:

1 × 12 = 12
2 × 6 = 12
3 × 4 = 12

So 12 is a Composite Number

And note this:

Any whole number greater than 1 is either Prime or Composite.
See Fundamental Theorem of Arithmetic .

Activity

You can try this Prime Numbers Activity.

Factors

We can also define a Prime Number using factors.

The numbers 2 and 3 pointing to 6 as its factors
"Factors" are numbers we multiply
together to get another number.

And we have:

When the only two factors of a number are 1 and the number,
then it is a Prime Number

It means the same as our previous definition, just stated using factors.

And remember this is only about Whole Numbers (1, 2, 3, ... and so on), not fractions or negative numbers. So don't say "I could multiply ½ times 6 to get 3", OK?

Examples:

3 = 1 × 3 (the only factors are 1 and 3)	Prime

6 = 1 × 6 6 = 2 × 3 (the factors are 1, 2, 3 and 6)	Composite

Examples From 1 to 14

Factors other than 1 or the number itself are highlighted:

Number	Can be Exactly Divided By	Prime, or Composite?
1	(1 isn't prime or composite)
2	1, 2	Prime
3	1, 3	Prime
4	1, 2, 4	Composite
5	1, 5	Prime
6	1, 2, 3, 6	Composite
7	1, 7	Prime
8	1, 2, 4, 8	Composite
9	1, 3, 9	Composite
10	1, 2, 5, 10	Composite
11	1, 11	Prime
12	1, 2, 3, 4, 6, 12	Composite
13	1, 13	Prime
14	1, 2, 7, 14	Composite
...	...	...

So when there are more factors than 1 or the number itself, the number is Composite.

A question for you: is 15 Prime or Composite?

Why All the Fuss about Prime and Composite?

A padlock superimposed on a background of binary code

Prime numbers help us keep our internet data secure using cryptography.

Based on the idea that multiplying primes together is much easier than figuring out which primes were multiplied to make a number.

We can "break apart" Composite Numbers into Prime Number factors.

Three toy blocks labeled 2, 2, and 3 stacked to represent prime factors

It is like the Prime Numbers are the basic building blocks of all numbers.

And the Composite Numbers are made up of Prime Numbers multiplied together.

Our diagram from before shows it in action:

Visual blocks for numbers 2 to 7, showing prime numbers as single blocks and composites as combined blocks

2 is Prime, 3 is Prime, 4 is Composite (=2×2), 5 is Prime, and so on...

Example: 12 is made by multiplying the prime numbers 2, 2 and 3 together.

12 = 2 × 2 × 3

The number 2 was repeated, which is OK.

In fact we can write it like this using the exponent of 2:

12 = 2² × 3

And that's why they are called "Composite" Numbers because composite means "something made by combining things"

There are many puzzles in mathematics that can be solved more easily when we "break up" the Composite Numbers into their Prime Number factors.

So, whether it's securing our online data or solving intriguing math puzzles, primes and composites play a fundamental role.

369, 1692, 1054, 1693, 2982, 2983, 2984, 3976, 2985, 3977