Long Division - Introduction

John and Ann are given $10 to share. How do they share it? Easy! $5 each.

But then they think of their little baby brother Max.

"Maybe we should share it with him?" they ask each other.

So how much do they each get?

$10 shared amongst 3 people

That's $3 each ... but 3 lots of $3 is $9:

That leaves $1 still to share.

Let's break that $1 into ten 10c pieces:

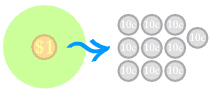
OK. Let's share those 10 cent pieces. That's an extra 30 cents each:

But that still leaves 10c !!!

So let's turn the 10c into ten 1c pieces:

OK, share that too: they each get 3c more:

That leaves one cent! But we can't break that cent any further so it
is simply "left over", which we call the "remainder"

The answer is: they each get $3 and another 30c and another 3c for a total of $3.33 each, with one cent left over!

$3.33 each (with a remainder of 1c)

And ...

That's how Long Division works!

In Long Division we:

• do the best division we can,
• then discover what's left over, and try to divide that,
• around and around until we can't go any further!

It is Written Down in a Special Way

First, we write down that we want to divide $10 by 3 like this:

Note: We don't use the $ symbol, instead we write
the $10 as the number 10.00 meaning 10 dollars and 0 cents

Then we write down that we took 3 lots of $3 to make $9:

We write the 9 below the 10, because the next thing to do is to subtract $9 from $10 to find we still have $1 left to divide:

Next is to repeat the whole thing, but do it for the $1 (which is written as 1.00):

That leaves 10 cents, or 0.10 yet to divide, so we repeat again:

We can't divide any more, so that's our answer!

$10 divided by 3 is $3.33 with $0.01 (1 cent) remainder

Now have a look at this Long Division Animation