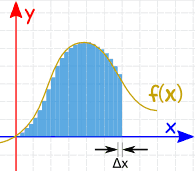
The study of how to get approximate answers by using lots of simple calculations. Used when direct perfect answers are hard.
Example: to find an area under a curve we can add up little rectangles.
Very useful in Engineering and Science when dealing with real world situations.
Example: to find how water flows through a town's pipe network (with pipes of different sizes and lengths, pumping stations, hills, valleys, etc) a computer can calculate approximate flows, then better calculate pressures, which alter the flows, then run it all again with the new flows, pressures, etc until it all balances out.
