Zero Product Property
The "Zero Product Property" says that:
If a × b = 0 then a = 0 or b = 0
(or both a=0 and b=0)
It can help us solve equations:
Example: Solve (x−5)(x−3) = 0
The "Zero Product Property" says:
If (x−5)(x−3) = 0 then (x−5) = 0 or (x−3) = 0
Now we just solve each of those:
For (x−5) = 0 we get x = 5
For (x−3) = 0 we get x = 3
And the solutions are:
x = 5, or x = 3
Here it is on a graph:
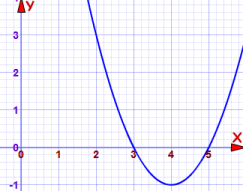
y=0 when x=3 or x=5
Standard Form of an Equation
Sometimes we can solve an equation by putting it into Standard Form and then using the Zero Product Property:
The "Standard Form" of an equation is:
(some expression) = 0
In other words, "= 0" is on the right, and everything else is on the left.
Example: Put x2 = 7 into Standard Form
Answer:
x2 − 7 = 0
This works because with the equation equal to 0 we can identify its factors. If the product of the factors is 0, then one or more of those factors must be 0.
Standard Form and the Zero Product Property
So let's try it out:
Example: Solve 5(x+3) = 5x(x+3)
We might be tempted to divide by (x+3), but this would mean dividing by zero when x = −3
So instead we can use "Standard Form":
5(x+3) − 5x(x+3) = 0
Which can be simplified to:
(5−5x)(x+3) = 0
5(1−x)(x+3) = 0
Then the "Zero Product Property" says:
(1−x) = 0, or (x+3) = 0
And the solutions are:
x = 1, or x = −3
And another example:
Example: Solve x3 = 25x
It is tempting to divide by x, but that is dividing by zero when x = 0
So let's use Standard Form and the Zero Product Property.
Bring all to the left hand side:
x3 − 25x = 0
Factor out x:
x(x2 − 25) = 0
x2 − 25 is a difference of squares, and can be factored into (x − 5)(x + 5):
x(x − 5)(x + 5) = 0
Now we can see three possible ways it could end up as zero:
x = 0, or x = 5, or x = −5
Summary of Steps
- Step 1: Write the equation in Standard Form (equal to 0)
- Step 2: Try to factor, if possible
- Step 3: If factored, use the Zero Product Property (set each factor equal to 0)
- Step 4: If can't be factoring try other ways (see Solving Equations)