Solving SSA Triangles

"SSA" means "Side, Side, Angle"

SSA Triangle

"SSA" is when we know two sides and an angle that is not the angle between the sides.

 

To solve an SSA triangle

 

Example 1

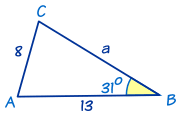
trig SSA example

In this triangle we know

  • angle B = 31°
  • b = 8
  • and c = 13

 

In this case, we can use The Law of Sines first to find angle C:

sin(C)/c = sin(B)/b
sin(C)/13 = sin(31°)/8
sin(C) = (13×sin(31°))/8
sin(C) = 0.8369...
C = sin−1(0.8369...)
C = 56.818...°   (* but see below)
C = 56.8° to one decimal place

Next, we can use the three angles add to 180° to find angle A:

A = 180° − 31° − 56.818...°
A = 92.181...° = 92.2° to one decimal place

Now we can use The Law of Sines again to find a:

a/sin(A) = b/sin(B)
a/sin(92.181...°) = 8/sin(31°)

Notice that we didn't use A = 92.2°, that angle is rounded to 1 decimal place. It's much better to use the unrounded number 92.181...° which should still be on our calculator from the last calculation.

a = (sin(92.181...°) × 8)/sin(31°)
a = 15.52 to 2 decimal places

So, we have completely solved the triangle ...

... or have we?

* Back when we calculated:

C = sin−1(0.8369...)
C = 56.818...°

We didn't include that sin−1(0.8369...) might have two answers (see Law of Sines):

The other answer for C is 180° − 56.818...°

Here you can see why we have two possible answers:

trig SSA example

By swinging side "8" left and right we can
join up with side "a" in two possible locations.

So let's go back and continue our example:

The other possible angle is:

C = 180° − 56.818...°
C = 123.2° to one decimal place

With a new value for C we will have new values for angle A and side a

Use "the three angles add to 180°" to find angle A:

A = 180° − 31° − 123.181...°
A = 25.818...°
A = 25.8° to one decimal place

Now we can use The Law of Sines again to find a:

a/sin(A) = b/sin(B)
a/sin(25.818...°) = 8/sin(31°)
a = (sin(25.818...°)×8)/sin(31°)
a = 6.76 to 2 decimal places

 

So the two sets of answers are:

C =  56.8°, A = 92.2°, a = 15.52

C = 123.2°, A = 25.8°, a = 6.76

 

Example 2

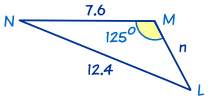
trig SSA example

This is also an SSA triangle.

In this triangle we know angle M = 125°, m = 12.4 and l = 7.6

We will use The Law of Sines to find angle L first:

sin(L)/l = sin(M)/m
sin(L)/7.6 = sin(125°)/12.4
sin(L) = (7.6×sin(125°))/12.4
sin(L) = 0.5020...
L = 30.136...°
L = 30.1° to one decimal place

Next, we will use "the three angles add to 180°" to find angle N:

N = 180° − 125° − 30.136...°
N = 24.863...°
N = 24.9° to one decimal place

Now we will use The Law of Sines again to find n:

n/sin(N) = m/sin(M)
n/sin(24.863...°) = 12.4/sin(125°)
n = (sin(24.863...°)×12.4)/sin(125°)
n = 6.36 to 2 decimal places

 

trig SSA example

Note there is only one answer in this case. The "12.4" line only joins up one place.

The other possible answer for L is 149.9°. But that is impossible because we already have M = 125° and a triangle can't have two angles greater than 90°.

Conclusion:

When solving a "Side, Side, Angle" triangle we start with the Law of Sines, but need to check if there is another possible answer!

 

267, 3960, 1529, 1549, 268, 1550, 1563, 2376, 2377, 3959
Triangle Solving Practice The Law of Sines The Law of Cosines Solving Triangles Trigonometry Index Algebra Index