Solving ASA Triangles

Example 1

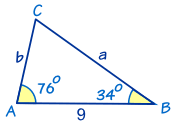
In this triangle we know:

• angle A = 76°
• angle B = 34°
• and c = 9

 

It's easy to find angle C by using 'angles of a triangle add to 180°':

C = 180° − 76° − 34° = 70°

 

We can now find side a by using the Law of Sines:

asin(A) = csin(C)

asin(76°) = 9sin(70°)

a = sin(76°) × 9sin(70°)

a = 9.29 to 2 decimal places

 

Similarly we can find side b by using the Law of Sines:

bsin(B) = csin(C)

bsin(34°) = 9sin(70°)

b = sin(34°) × 9sin(70°)

b = 5.36 to 2 decimal places

Now we have completely solved the triangle: we have found all angles and sides.

Example 2

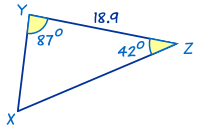
This is also an ASA triangle.

First find angle X by using 'angles of a triangle add to 180°':

X = 180° − 87° − 42° = 51°

Now find side y by using the Law of Sines:

ysin(Y) = xsin(X)

ysin(87°) = 18.9sin(51°)

y = sin(87°) × 18.9sin(51°)

y = 24.29 to 2 decimal places.

Similarly we can find z by using the Law of Sines:

zsin(Z) = xsin(X)

zsin(42°) = 18.9sin(51°)

z = sin(42°) × 18.9sin(51°)

z = 16.27 to 2 decimal places.

All done!