Derivation of Quadratic Formula

Let us find out how the famous Quadratic Formula can be created using a bunch of algebra steps.

And it can be solved using the Quadratic Formula:

That formula looks like magic, but you can follow the steps to see how it comes about.

1. Complete the Square

ax² + bx + c has "x" in it twice, which is hard to solve.

But there is a way to rearrange it so that "x" only appears once. It is called Completing the Square (please read that first!).

Our aim is to get something like x² + 2dx + d², which can then be simplified to (x+d)²

So, let's go:

Start with $ax^2 + bx + c=0$

Divide the equation by a $x^2 + bx/a + c/a = 0$

Put c/a on other side $x^2 + bx/a = -c/a$

Add (b/2a)² to both sides $x^2 + bx/a + (b/2a)^2 = -c/a + (b/2a)^2$

The left hand side is now in the x² + 2dx + d² format, where "d" is "b/2a". So we can re-write it this way:

"Complete the Square" $(x+b/2a)^2 = -c/a + (b/2a)^2$

Now x only appears once and we are making progress.

We will try to rearrange the equation to have just "x" on the left:

Start with $(x+b/2a)^2 = -c/a + (b/2a)^2$

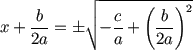
Square root both sides $(x+b/2a) = (+-) sqrt(-c/a+(b/2a)^2)$

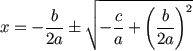
Move b/2a to right $x = -b/2a (+-) sqrt(-c/a+(b/2a)^2)$

x is on its own!
but let's simplify

Multiply right by 2a/2a $x = [ -b (+-) sqrt(-(2a)^2 c/a + (2a)^2(b/2a)^2) ] / 2a$

Simplify inside root $x = [ -b (+-) sqrt(-4ac + b^2) ] / 2a$

Which is the Quadratic formula we all know and love:

Quadratic Formula: x = [ -b (+-) sqrt(b^2 - 4ac) ] / 2a