Even and Odd Functions

They are special types of functions

Even Functions

A function is "even" when:

f(x) = f(−x) for all x

In other words there is symmetry about the y-axis (like a reflection):

This is the curve f(x) = x²+1

They are called "even" functions because the functions x², x⁴, x⁶, x⁸, etc behave like that, but there are other functions that behave like that too, such as cos(x):

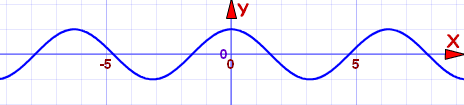
Cosine function: f(x) = cos(x)
It is an even function

But an even exponent does not always make an even function, for example (x+1)² is not an even function.

Odd Functions

A function is "odd" when:

−f(x) = f(−x) for all x

Note the minus in front of f(x): −f(x).

And we get origin symmetry:

This is the curve f(x) = x³−x

They are called "odd" because the functions x, x³, x⁵, x⁷, etc behave like that, but there are other functions that behave like that, too, such as sin(x):

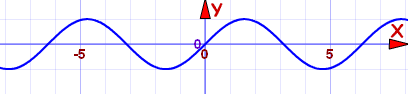
Sine function: f(x) = sin(x)
It is an odd function

But an odd exponent does not always make an odd function, for example x³+1 is not an odd function.

Neither Odd nor Even

Don't be misled by the names "odd" and "even" ... they are just names ... and a function does not have to be even or odd.

In fact most functions are neither odd nor even. For example, just adding 1 to the curve above gets this:

This is the curve f(x) = x³−x+1

It is not an odd function, and it is not an even function either.
It is neither odd nor even

Even or Odd?

Even and Odd

The only function that is even and odd is f(x) = 0

Special Properties

Adding:

• The sum of two even functions is even
• The sum of two odd functions is odd
• The sum of an even and odd function is neither even nor odd (unless one function is zero).

Multiplying:

• The product of two even functions is an even function.
• The product of two odd functions is an even function.
• The product of an even function and an odd function is an odd function.