Using Exponents in Algebra
You might like to read the page on Exponents first.
Whole Number Exponents
The exponent "n" in an says
how many times to use a in a multiplication:
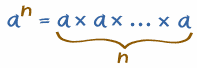
Example: 53 = 5 × 5 × 5 = 125
- The "3" says to use 5 three times in a multiplication
- In words: 53 could be called "5 to the third power", "5 to the power 3" or simply "5 cubed"
Negative Exponents
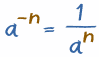
A negative exponent a-n is equal to 1/an (1 divided by the positive exponent)
Example:
5-3 = 1/53 = 1/125 = 0.008
Also ... by changing the signs of the exponents we get:
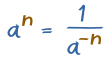
A positive exponent an is equal to 1/a-n (1 divided by the negative exponent)
So, we can move an expression between the top and bottom (numerator and denominator) of a fraction when we also change the sign of the exponent.
Example: x-1 = 1/x (a simple reciprocal)
Example: 5-3 = 1/53 = 1/125 = 0.008
Positive and Negative Together
Here is an example with positive and negative exponents:
Example: 432-59-132
We can put the values with negative exponents at the bottom (remembering to make the exponents positive):
4332259
Let's simplify it!
32 is 9:
439259
The 9s cancel out:
4325
43 is 4 × 4 × 4 = 64, and
25 is 2 × 2 × 2 × 2 × 2 = 32:
6432
Which simplifies to:
2
Done!