Approximate Solutions
Sometimes it is difficult to solve an equation exactly, but an approximate answer may be good enough.
What's Good Enough?
Well, that depends what we are working on!
- If we are dealing with millions of dollars then we should try to get pretty close indeed. And that might need many significant digits
- If we are calculating how much food to buy for a party, then a small error won't matter so much. We could always buy a little extra to be sure
- Or something in between
So understanding what we are working on helps us know how accurate we should be.
Example: Cooking
For general cooking we can change things a bit and get away with it. Adding an extra 50g of carrot is fine. Just not too much salt, please!

Example: Baking
When baking a cake, small changes in ingredients are often fine, a little extra cocoa or slightly less sugar is OK, but if we go too far the result may be a failure.
Adding 100ml extra milk will make the result wet and yucky.
Example: Aerospace Engineering
Calculations for the trajectory and fuel needs of spacecraft require extreme accuracy. Small errors can lead to going off-course and mission failure.
Solving Equations
We still want to be as accurate as possible, so try to handle any approximate data sensibly.
When solving equations:
- first get it in the form x = something
- then do any calculations
Like this:
Example: Solve x/7 − 6.3068 + 2π = 0 (to 3 decimal places)
Checking
If our answer is approximate, then our checking will also be approximate.
Example: Check that x = 0.165 solves x/7 − 6.3068 + 2π = 0
Not quite right, but very close.
Graphical Estimation
We can make good approximations using graphs, particularly by using a zoom function, like on the Function Grapher.
Here's an example:
Example: estimate the solution to x3 − 2x2 − 1 = 0 (to 2 decimal places).
Solution: Plot it!
Here's my first attempt. I can see it crosses through y=0 at about x=2.2
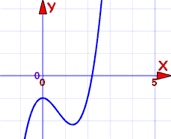
Let's zoom in there to see if we can see the crossing point better:
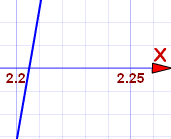
It crosses between 2.20 and 2.21 ... slightly closer to 2.21. We are asked for 2 decimal places, so our answer is:
x3 − 2x2 − 1 = 0 at about x = 2.21
Check: (2.21)3 − 2(2.21)2 − 1 ≈ 0.026, which is very close to 0.