Activity: Drawing Squares

For this activity all you need is a grid of dots, a pencil and your brain.

Let us discover how many squares you can make on different grids:

grids 1x1, 2x2, 3x3, etc

Note: "1 by 1" means how many sides (not how many dots).


So, let's try drawing in some squares and count how many:

1 by 1

Well, that's easy, there's just one:   squares3

2 by 2

That seems to be easy too. There are four of them, aren't there?  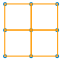 squares4
     
But wait, that's not the complete answer.
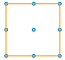There's also this bigger one:		   squares5

That makes five squares altogether - four 1 by 1 squares and one 2 by 2 square

Your Turn !

3 by 3

Over to you now.

Here's the grid:

   squares6

Hint: For the 3 by 3 case, you will expect to get 1 by 1 squares, 2 by 2 squares and 3 by 3 squares. How many of each?



squares grid


 

Now you can start to fill in a table:

  How Many
1 by 1 squares		 How Many
2 by 2 squares		 How Many
3 by 3 squares		 How Many
4 by 4 squares		 How Many
5 by 5 squares		 Total
1 by 1 Grid: 1



1
2 by 2 Grid: 4 1


5
3 by 3 Grid:





4 by 4 Grid:





5 by 5 Grid:





 

Did you notice anything about the numbers in the table?

They are all square numbers:

and the totals are found by adding together square numbers.

Formula to The Rescue ... !

There is actually a formula for adding the first n square numbers:

Sn = n(n+1)(2n+1) / 6

Example: The number of squares in the 5 by 5 case

Try substituting n = 5 into the formula:

Sn = n(n+1)(2n+1) / 6
S5 = 5 × (5+1) × (2×5+1) / 6
S5 = 5 × 6 × 11 / 6
S5 = 55

 

So, we seem to have solved the question. Yipee!

But wait ... there's more!

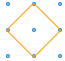
I said you would need to use your brains. Let's go back to the 2 by 2 case:

2 by 2

There is another square too, this one:

squares9

Why is it a square? It has four equal sides and four right angles, so that's a square.

So, that makes six squares altogether.

Four 1 by 1 squares, one 2 by 2 square and one x by x square.

What is the value of x? We can use Pythagoras' Theorem to find it:

x2 = 12 + 12 = 1 + 1 = 2
So x =  √2

So, we have four 1 by 1 squares, one 2 by 2 square and one √2 by √2 square.

Your Turn !

3 by 3

YES! Can you find them?

4 by 4 and 5 by 5

Also try the 4 by 4 grid, and the 5 by 5 grid

As you proceed, you will find squares like these:

tilted squares

 

What are the lengths of the sides of these squares?

You can use Pythagoras' Theorem to work that out yourself

In each case, how many do you get of each one?

Here is a table to help you:

  How Many
1 by 1 		How Many
2 by 2 		How Many
3 by 3 		How Many
4 by 4 		How Many
5 by 5 		How Many
√2 by
 √2 		How Many
√5 by √5 		How Many
√8 by √8 		How Many
√10 by √10		 How Many
√13 by √13 		How Many
√17 by √17		 Total
1 by 1 Grid: 1









1
2 by 2 Grid: 4 1


1  



6
3 by 3 Grid:











4 by 4 Grid:











5 by 5 Grid:











 

Advanced

Can you find a formula to calculate the number of squares that have lengths that are square roots?

Can you then find a formula for the total number of squares in each case?

Are there any more squares lurking in there that we've missed?

Conclusion

What started off as seeming to be a simple exercise turned out to be quite complex. You really do need to use your brains to think this one through, but it's a challenging and rewarding exercise.

 

Activity Index