Solving SSS Triangles

"SSS" means "Side, Side, Side"

"SSS" is when we know three sides of the triangle, and want to find the missing angles.

To solve an SSS triangle:

• use The Law of Cosines first to calculate one of the angles
• then use The Law of Cosines again to find another angle
• and finally use angles of a triangle add to 180° to find the last angle

We use the "angle" version of the Law of Cosines:

cos(C) = a² + b² − c²2ab

cos(A) = b² + c² − a²2bc

cos(B) = c² + a² − b²2ca

(they are all the same formula, just different labels)

Example 1

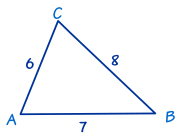
In this triangle we know the three sides:

• a = 8,
• b = 6 and
• c = 7

Use the Law of Cosines first to find one of the angles. It doesn't matter which one. Let's find angle A first:

cos(A) = (b² + c² − a²) / 2bc

cos(A) = (6² + 7² − 8²) / (2×6×7)

cos(A) = (36 + 49 − 64) / 84

cos(A) = 0.25

A = cos^-1(0.25)

A = 75.5224...°

A = 75.5° to one decimal place.

Next we find another angle. We use the Law of Cosines again, this time for angle B:

cos(B) = (c² + a² − b²)/2ca

cos(B) = (7² + 8² − 6²)/(2×7×8)

cos(B) = (49 + 64 − 36) / 112

cos(B) = 0.6875

B = cos^-1(0.6875)

B = 46.5674...°

B = 46.6° to one decimal place

Finally, we can find angle C by using "angles of a triangle add to 180°":

C = 180° − 75.5224...° − 46.5674...°

C = 57.9° to one decimal place

Now we have completely solved the triangle ... we have found all its angles.

The triangle can have letters other than ABC:

Example 2

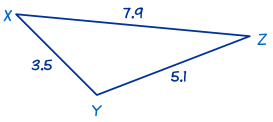
This is also an SSS triangle.

In this triangle we know the three sides x = 5.1, y = 7.9 and z = 3.5. Use The Law of Cosines to find angle X first:

cos(X) = (y² + z² − x²)/2yz

cos(X) = ((7.9)² + (3.5)² − (5.1)²)/(2×7.9×3.5)

cos(X) = (62.41 + 12.25 − 26.01)/55.3

cos(X) = 48.65/55.3 = 0.8797...

X = cos^-1(0.8797...)

X = 28.3881...°

X = 28.4° to one decimal place

Next we'll use The Law of Cosines again to find angle Y:

cos(Y) = (z² + x² − y²)/2zx

cos(Y) = (3.5² + 5.1² − 7.9²) / (2 × 3.5 × 5.1)

cos(Y) = (12.25 + 26.01 − 62.41)/35.7

cos(Y) = −24.15/35.7 = −0.6764...

Y = cos^-1(−0.6764...)

Y = 132.5684...°

Y = 132.6° to one decimal place.

Finally, we can find angle Z by using "angles of a triangle add to 180°":

Z = 180° − 28.3881...° − 132.5684...°

Z = 19.0° to one decimal place

Another Method

Here's another (slightly faster) way to solve an SSS triangle:

• use the Law of Cosines first to calculate the largest angle
• then use the Law of Sines to find another angle
• and finally use angles of a triangle add to 180° to find the last angle

Largest Angle?

Why do we try to find the largest angle first? That way the other two angles must be acute (less than 90°) and the Law of Sines will give correct answers.

So by calculating the largest angle first using the Law of Cosines, the other angles are less than 90° and the Law of Sines can be used on either of them without difficulty.