Solving Rational Inequalities

Rational

A Rational Expression looks like:

A fraction where the numerator is a polynomial and the denominator is a polynomial.

Inequalities

Sometimes we need to solve rational inequalities like these:

Symbol Words Example
> greater than (x+1)/(3−x) > 2
< less than x/(x+7) < −3
≥ greater than or equal to (x−1)/(5−x) ≥ 0
≤ less than or equal to (3−2x)/(x−1) ≤ 2

Solving

Solving inequalities is very like solving equations ... we do most of the same things.

Graph of a rational function showing intervals where the function is positive (above x-axis) or negative (below x-axis).
When we solve inequalities
we try to find interval(s),
such as the ones marked "<0" or ">0"

These are the steps:

  • 1. Simplify the inequality so that one side is 0 (for example, f(x) > 0 or f(x) < 0)
  • 2. Find "points of interest":
    • the "=0" points (roots), and
    • where the function is undefined (vertical asymptotes)
  • 3. In between the "points of interest", the function is either greater than zero (>0) or less than zero (<0)
    • choose a test value from each interval to see if it is >0 or <0

Here is an example:

Example: 3x−10x−4 > 2

First, let's simplify!

But We Cannot Multiply By (x−4)

If we multiply both sides of an inequality by a negative number, we must reverse the inequality sign. But we don't know if (x−4) is positive or negative (it depends on x), so we don't know whether to reverse the sign or not (see Solving Inequalities.)

Instead, bring "2" left:

3x−10x−4 − 2 > 0

Then multiply the 2 by (x−4)/(x−4):

3x−10x−4 − 2x−4x−4 > 0

Now we have a common denominator, let's bring it all together:

3x−10 − 2(x−4)x−4 > 0

Simplify:

x−2x−4 > 0

Second, let's find "points of interest".

At x=2 we have: (0)/(x−4) > 0, which is a "=0" point, or root

At x=4 we have: (x−2)/(0) > 0, which is undefined

Third, do test points to see what it does in between:

At x=0:

  • x−2 = −2, which is negative
  • x−4 = −4, which is also negative
  • So (x−2)/(x−4) must be positive

We can do the same for x=3 and x=5 (or any other values in those intervals), and end up with these results:

  x=0 x=2 x=3 x=4 x=5
x−2 < 0   > 0   > 0
x−4 < 0   < 0   > 0
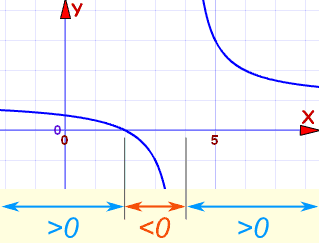
(x−2)/(x−4) is > 0 0 < 0 undefined > 0

That gives us a complete picture!

And where is it > 0 ?

  • Less than 2
  • Greater than 4

So, after rearranging and analysing 3x−10x−4 > 2 we get the result for x:

(−∞, 2) U (4, +∞)

We did all that without drawing a plot!

But here is the plot of (x−2)/(x−4) so we can see:

Graph of the rational function y=(x-2)/(x-4) showing an x-intercept at x=2 and a vertical asymptote at x=4.

581, 582, 9046, 1230, 9047, 2282, 9048, 1231, 9049, 2283
Inequalities Less Than or Greater Than