Solving SAS Triangles

"SAS" means "Side, Angle, Side"

Triangle with two sides and the included angle highlighted to represent Side-Angle-Side.

"SAS" is when we know two sides and the angle between them.

To solve an SAS triangle

Example 1

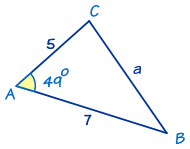
Triangle with sides of 5 and 7 and an included angle of 49 degrees.

In this triangle we know:

  • angle A = 49°
  • side b = 5, and
  • side c = 7

To solve the triangle we need to find side a and angles B and C.

Use The Law of Cosines to find side a first:

a2 = b2 + c2 − 2bc cosA

a2 = 52 + 72 − 2 × 5 × 7 × cos(49°)
a2 = 25 + 49 − 70 × cos(49°)
a2 = 74 − 70 × 0.6560...
a2 = 74 − 45.924... = 28.075...
a = √28.075...
a = 5.298...
a = 5.30 to 2 decimal places

Now we use the Law of Sines to find the smaller of the other two angles.

Why the smaller angle? Because the inverse sine function gives answers less than 90° even for angles greater than 90°. By choosing the smaller angle (a triangle won't have two angles greater than 90°) we avoid that problem. Note: the smaller angle is the one facing the shorter side.

Choose angle B:

sin Bb = sin Aa

sin B5 = sin(49°)5.298...
Did you notice that we didn't use a = 5.30. That number is rounded to 2 decimal places. It is much better to use the unrounded number 5.298... which should still be on our calculator from the last calculation.
sin B = sin(49°) × 55.298...
sin B = 0.7122...
B = sin-1(0.7122...)
B = 45.4° to one decimal place

Now we find angle C, which is easy using 'angles of a triangle add to 180°':

C = 180° − 49° − 45.4°
C = 85.6° to one decimal place

Now we have completely solved the triangle ... we have found all its angles and sides.

Example 2

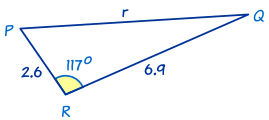
Obtuse triangle with sides 6.9 and 2.6 and an included angle of 117 degrees.

This is also an SAS triangle.

First let's find r using The Law of Cosines:

r2 = p2 + q2 − 2pq cos R

r2 = 6.92 + 2.62 − 2 × 6.9 × 2.6 × cos(117°)
r2 = 47.61 + 6.76 − 35.88 × cos(117°)
r2 = 54.37 − 35.88 × (−0.4539...)
r2 = 54.37 + 16.289... = 70.659...
r = √70.659...
r = 8.405... = 8.41 to 2 decimal places

Now for The Law of Sines.

Choose the smaller angle? We don't have to! Angle R is greater than 90°, so angles P and Q must be less than 90°.

sin Pp = sin Rr

sin P6.9 = sin(117°)8.405...
sin P = sin(117°) × 6.98.405...
sin P = 0.7313...
P = sin-1(0.7313...)
P = 47.0° to one decimal place

Now we will find angle Q using 'angles of a triangle add to 180°':

Q = 180° − 117° − 47.0°
Q = 16.0° to one decimal place

All Done!

Mastering this skill needs lots of practice, so try these questions:

265, 3961, 1546, 266, 1547, 1548, 1562, 2374, 2375, 3962
Solving Triangles Triangle Solving Practice The Law of Sines The Law of Cosines Trigonometry Index Algebra Index