Axioms, Theorems, Corollaries, Lemmas

What are all those things? They sound so impressive!

Well, they are basically just facts: statements that have been proven to be true (or accepted as true).

An Axiom (or Postulate) is a starting rule we accept as true without proof
A Theorem is a major result (proved using axioms and earlier results)
A Corollary is a result that follows directly from a theorem
A Lemma is a result proved mainly to help prove another theorem
A Conjecture is an idea we think is true but haven't proven yet. Once a conjecture is proven, it becomes a theorem!

Note: A result is called a lemma because of how it is used, not because it is small.

Examples

Example: An Axiom

Axiom: In basic geometry: through any two points there's exactly one straight line.

This isn't proved, it is a starting rule we agree to use.

All proofs are built on axioms: without them there would be nowhere to start.

Example: A Theorem and a Corollary

Theorem:

Angles on one side of a straight line always add to 180°.

Straight line with two adjacent angles a and b adding to 180 degrees

Corollary:

From this theorem we can show that when two lines intersect, the angles opposite each other (called Vertical Angles) are equal.

Two intersecting lines forming four angles: a and c are opposite, b and d are opposite
Angle a = angle c
Angle b = angle d

Proof:

Angles a and b lie on a straight line, so:

a + b = 180°

a = 180° − b

Likewise for angles b and c:

b + c = 180°

c = 180° − b

Since both a and c equal 180° − b, we have:

a = c

And a slightly more complicated example from Geometry:

Example: A Theorem with Corollaries

Theorem:

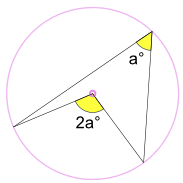
Circle with central angle 2a and an inscribed angle a sharing the same arc

An inscribed angle a° is half of the central angle 2a°

Called the Angle at the Center Theorem.

Proof:

Join the center O to A.

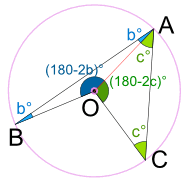
inscribed angle proof

Triangle ABO is isosceles (two equal sides, two equal angles), so:

Angle OBA = Angle BAO = b°

And, using Angles of a Triangle add to 180°:

Angle AOB = (180 − 2b)°

Triangle ACO is also isosceles, so:

Angle OCA = Angle CAO = c°

Using Angles of a Triangle add to 180°:

Angle AOC = (180 − 2c)°

Using Angles around a point add to 360°:

Angle BOC = 360° − (180 − 2b)° − (180 − 2c)° = 2b° + 2c° = 2(b + c)°

Since b + c = a, we get:

Angle BAC = a° and Angle BOC = 2a°

Circle with central angle 2a and an inscribed angle a sharing the same arc

And so the theorem is proved.

Corollary

If the endpoints stay the same, then the inscribed angle is always the same, no matter where it is on the circle:

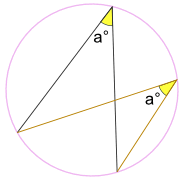
inscribed angle a and a

So, angles subtended by the same arc are equal.

This is usually called the Angles Subtended by the Same Arc Theorem, but it follows directly from the Angle at the Center Theorem, so is a corollary.

Corollary (Special Case): Angle in a Semicircle

In the special case where the central angle forms a diameter of the circle:

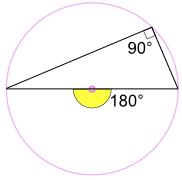
Circle with central angle 2a and an inscribed angle a sharing the same arc angle semicircle 180 and 90

2a° = 180° , so a° = 90°

So an angle inscribed in a semicircle is always a right angle.

Another example, related to Pythagoras' Theorem:

Example: Pythagoras

Theorem

If m and n are any two whole numbers and

a = m² − n²
b = 2mn
c = m² + n²

then

a² + b² = c²

Proof:

a² + b² = (m² − n²)² + (2mn)² = m⁴ − 2m²n² + n⁴ + 4m²n² = m⁴ + 2m²n² + n⁴ = (m² + n²)² = c²

Corollary

a, b and c, as defined above, are a Pythagorean Triple

This follows directly from theorem.

Example (A Specific Case)

If m = 2 and n = 1, then

a = 2² − 1² = 4 − 1 = 3
b = 2 × 2 × 1 = 4
c = 2² + 1² = 4 + 1 = 5

So 3, 4, and 5 form a Pythagorean triple.