The Law of Cosines

 

For any triangle ...

triangle angles A, B, C and sides a, b, c

a, b and c are sides.

C is the angle opposite side c

... the Law of Cosines (also called the Cosine Rule) says:

c2 = a2 + b2 − 2ab cos(C)

It helps us solve some triangles. Let's see how to use it.

Example: How long is side "c" ... ?

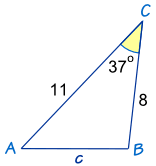
trig cos rule example

We know angle C = 37º, and sides a = 8 and b = 11

The Law of Cosines says:c2 = a2 + b2 − 2ab cos(C)
Put in the values we know:c2 = 82 + 112 − 2 × 8 × 11 × cos(37º)
Do some calculations:c2 = 64 + 121 − 176 × 0.798…
More calculations:c2 = 44.44...
Take the square root:c = √44.44 = 6.67 to 2 decimal places


Answer: c = 6.67

How to Remember

How can you remember the formula?

Well, it helps to know it's the Pythagoras Theorem with something extra so it works for all triangles:

Pythagoras Theorem:
(only for Right-Angled Triangles)a2 + b2 = c2
Law of Cosines:
(for all triangles)a2 + b2 − 2ab cos(C) = c2

So, to remember it:

When to Use

The Law of Cosines is useful for finding:

  • the third side of a triangle when we know two sides and the angle between them (like the example above)
  • the angles of a triangle when we know all three sides (as in the following example)

Example: What is Angle "C" ...?

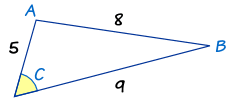
trig cos rule example

The side of length "8" is opposite angle C, so it is side c. The other two sides are a and b.

Now let us put what we know into The Law of Cosines:

Start with:c2 = a2 + b2 − 2ab cos(C)
Put in a, b and c:82 = 92 + 52 − 2 × 9 × 5 × cos(C)
Calculate:64 = 81 + 25− 90 × cos(C)

Now we use our algebra skills to rearrange and solve:

Subtract 25 from both sides:39 = 81− 90 × cos(C)
Subtract 81 from both sides:−42 = −90 × cos(C)
Swap sides:−90 × cos(C) = −42
Divide both sides by −90:cos(C) = 42/90
Inverse cosine:C = cos-1(42/90)
Calculator:C = 62.2° (to 1 decimal place)

In Other Forms

Easier Version For Angles

We just saw how to find an angle when we know three sides. It took quite a few steps, so it is easier to use the "direct" formula (which is just a rearrangement of the c2 = a2 + b2 − 2ab cos(C) formula). It can be in either of these forms:

cos(C) = a2 + b2 − c2 2ab

cos(A) = b2 + c2 − a2 2bc

cos(B) = c2 + a2 − b2 2ca

Example: Find Angle "C" Using The Law of Cosines (angle version)

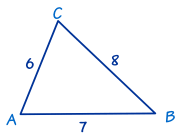
triangle SSS

In this triangle we know the three sides:

  • a = 8,
  • b = 6 and
  • c = 7.

Use The Law of Cosines (angle version) to find angle C :

cos C= (a2 + b2 − c2)/2ab
 = (82 + 62 − 72)/2×8×6
 = (64 + 36 − 49)/96
 = 51/96
 = 0.53125
C= cos-1(0.53125)
 = 57.9° to one decimal place

 

Versions for a, b and c

Also, we can rewrite the c2 = a2 + b2 − 2ab cos(C) formula into a2= and b2= form.

Here are all three:

a2 = b2 + c2 − 2bc cos(A)

b2 = a2 + c2 − 2ac cos(B)

c2 = a2 + b2 − 2ab cos(C)

But it is easier to remember the "c2=" form and change the letters as needed.

As in this example:

Example: Find the distance "z"

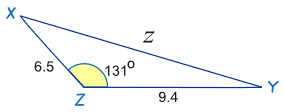
trig cos rule example

The letters are different! But that doesn't matter. We can easily substitute x for a, y for b and z for c

Start with:c2 = a2 + b2 − 2ab cos(C)
x for a, y for b and z for cz2 = x2 + y2 − 2xy cos(Z)
Put in the values we know:z2 = 9.42 + 6.52 − 2×9.4×6.5×cos(131º)
Calculate:z2 = 88.36 + 42.25 − 122.2 × (−0.656...)
 z2 = 130.61 + 80.17...
 z2 = 210.78...
 z = √210.78... = 14.5 to 1 decimal place.

Answer: z = 14.5

Did you notice that cos(131º) is negative and so the last term ends up positive (+ 80.17...)

The cosine of an obtuse angle is always negative (see Unit Circle).

 

1512, 1513, 1514, 1515, 1516, 1517,254,255, 2380, 2381
The Law of Sines Solving Triangles Trigonometry Index Algebra Index